Introduction
This document will describe the basic
operation and application of the Leica Total Station surveying equipment
as well as discuss the process of downloading the data and producing
detailed topography maps using the Liscad software. It is meant to
explain the operation based upon the Active Tectonics members’
experiences in using the equipment, and should supplement the reading of
the manual and your intuition. This document contains the basic set-up
and operating instructions for our electronic surveying equipment. It
also contains discussions of how the instrument works, and suggestions for
methods and strategies of use.
Equipment
Description
Most of this equipment is stored in the
locked cabinet, or alongside it, in the Active Tectonics lab, room 475 of
the Physical Sciences H-wing. An equipment list and check out sheet are
posted on the door of the cabinet.
Table 1. Location of the Total Staion and its components.
Picture of all items and associated checklist.
|
Item |
Description/Location |
|
Leica (Wild) TCM-1100 self-contained Motorized Coaxial
Electronic Total Station |
This is the core of the surveying equipment, controlling the EDM (Electromagnetic Distance
Measurement device), manipulating and storing the data, and measuring
horizontal and vertical angles. It has an optical plumb for centering
over a station and two levels. The EDM is implemented around the
theodolite's telescope so both sighting optics are coaxial. The EDM measures the slope distance to the
reflector, and communicates the data to the theodolite. We have two
TCM-1100 that
are kept in the cabinet in H475. |
|
Reflector |
Corner-cube type. Two of these, along with a
reflector cap, are kept alongside the cabinet in H475. |
|
Plumbing pole/reflector staff |
The reflector attaches to the top of this and it
telescopes in height from 1.30 m to 2.15 m. It is light and a useful
alpine staff, although Roland Bürgmann stabbed himself before on the
pointed bottom of a similar plumb pole, so be careful. Two of these are
kept alongside the cabinet in H475. |
|
Tripod for Theodolite |
Two of these are kept alongside the cabinet in
H475. |
|
Small Internal Batteries |
We have two small batteries. They are inserted into
a compartment on the side of the Total Station. Each of these when fully
charged within a few days of the survey effort should be good for at least
300 to 800 shots, depending on use of motors. Each small battery weighs ?
kg (? lb). These are kept in the locked cabinet or in its compartment in
the Total Station. |
|
Gel-cell Batteries and cords |
The gel-cell batteries can support the
Total Station for 7x the time of the internal battery. They weigh about 8 pounds (3.5 kg).
They can be left on the smart charger indefinitely. We have two of these, along with padded cases.
We also have two cords that plug into the side of the Total Station where a gutted battery takes
place of the real one. These are also found in the locked cabinet in H475. This battery system owes its origination to Lee Amoroso, our battery specialist.
|
|
Battery Charger |
Two that plug into an electrical outlet; two that run off the car battery
|
|
Cables (see checklist) |
Rechargeable battery (gel-cell) to Total Station (2);
outlet to Total Station(2);
adapter cable for inverter(2). |
|
Portable Power Inverter |
We have two for the batteries. |
|
International Adapter Plugs |
important if traveling overseas (2 sets). |
|
Strip Surge Suppressor |
We have two. |
|
Verbatim SRAM Card 2MB(I think it stands for Static
Read-Only Memory, but check)
|
The SRAM card acts as a memory module for
coordinates and attributes
recorded with the Total Station. SRAM cards can hold variable amounts
of data (e.g., 2 MB SRAM cartridges, 8 MB cartridges, etc.) and allow for
the Total Station operator to collect a large amount of data, given that
s/he has enough SRAM cards to store the project's work. The SRAM card
interfaces with a PC via the PCMCIA port; therefore, transfer of data is
quick and easy. A 2MB SRAM card is capable of storing approximately 8000
blocks of data.
|
|
2-Way Radios |
We have 4 Motorola Radius SP50 and 4 BELL Phones
(#9914-1) FRS UHF 2-Way Radios |
Leica (Wild) Surveying Equipment
The Leica (Wild) equipment is well
known as some of the best surveying equipment available. It is often
referred to as "the Cadillac" of surveying equipment. "All surveyors
either own a Leica (Wild) or wish that they did" (Hanz Haselbach, Jr.,
personal communication, 1991). Leica (Wild) makes top of the line
equipment that is used on all expeditions and has better mechanics,
optics, factory support, ease of repair, and ability to maintain resale
value than other manufacturers. Furthermore, the company supports older
equipment by providing a modular set-up, allowing selective upgrades:
We bought our system from:
Surveyor’s Service Company
4317 N. 16th Street
Phoenix, AZ 85016
(800) 938-0608
(602) 274-2052
They should be consulted for upgrades, repairs or with
questions.
Preparation
In order to properly prepare for a
survey effort, checking the equipment in the lab/office before leaving and
proper reconnaissance before set up are important. On the next page is a
list of equipment and the checks that should be made before leaving the
office.
Planning and Reconnaissance
Before leaving the office, look at the base map or airphoto of
the area and define the mapping project(s). Consider access. If you need
permission to get on the property, you should get that well in advance.
The equipment is heavy and bulky. Two people can carry it with difficulty
for 1 or 2 kilometers, but it is a demoralizing experience. Therefore,
try to plan appropriate vehicle access, but don't drive unnecessarily
through the landscape destroying the beauty and making a bad name for
geologists! You must have a field assistant. Operating this equipment by
yourself is pretty silly, although it can be done. You will end up
walking at least two times the total slope length of the shots you make.
The distance will add up quickly! Your helper need not be a geologist,
but should be sturdy, careful, and interested.
Once in the field, walk over the area with the field assistant.
Look for suitable instrument stations. Much time and precision may be
lost with multiple set ups. Therefore, plan the minimum number of
instrument stations. A high position somewhere near the survey area
should suffice. Remember that the instrument has an effective working
range of at least 1 km, so if you have walkie-talkies or body signals and can communicate
(see communication techniques) over long ranges, much of the survey
may be completed from a single well chosen site. Consider gullies and
ridges, and other obstacles that may obscure the survey. Remember that
the reflector plumb staff telescopes to 2.15 m, so that may help
with visibility. Be sure to communicate to the instrument operator
changes in reflector height (click here to see how to enter into Total Station)
and record them on the Survey Record Form and
in the Thoedolite! While reconnoitering the area, consider the problem
being addressed by the mapping project, and choose an appropriate and
optimal strategy: What is the optimum number and distribution of points
necessary for this project? What is the desired precision? Will I ever
want to reoccupy this network? Be sure that the field assistant
understands the strategy too, so that you do not have to have major
discussions about strategy once you have started working, although the
plan should be flexible if an obvious modification becomes apparent.
Table 2. Equip and location.
|
Y |
Item |
Check/comments |
| |
Essential Total Station
Equipment: Total Station and parts photo checklist |
| |
Theodolite |
Check smoothness of horizontal and vertical
spindles. Turn on and off to check electronics. |
| |
Tripod |
Set up and make sure that it opens smoothly.
There should be no play between the various components. If necessary,
moderately tighten the three Allen screws under the tripod plate. When
the tripod is lifted by its head, the legs should just remain spread out.
Adjust the hinge screws if necessary. The yellow plastic head cover for
the tripod contains an Allen key for the tripod screws. |
| |
Verbatim SRAM card |
This is the memory. It should be stored in
the side of the Theodolite in its compartment. Check with previous users
of the instrument to determine if they have backed up any data they might
need in the module so you can clear it if necessary before starting your
survey. Note: It must be inscerted correctly: Look at the front with the
right-side-up and that side goes on the bottom of the case.
So when the case is shut the front is facing the outside of the
Total Station and it is right-side-up. |
| |
Reflector |
Ensure it is clean and stored in a clean place. |
| |
Reflector plumb staff |
Make sure it telescopes smoothly. |
| |
Batteries |
Ensure that at least one of the large ones
has been charged. To fully charge, it may take 8 to 12 hours. Also charge
the on board battery on the Total Station. |
| |
Computer |
Optional. Make sure that you have all of the
cables and parts (mouse, keyboard, etc.). Software necessary for Liscad
plots include Excel, Canvas, Liscad, and the Liscad dongle. Bring some floppy disks to back up
data in a few places. |
| |
Brunton Compass |
Used to approximately level the instrument,
and to determine reference azimuth. |
| |
Backpack, Briefcase |
These should be loaded up with the
gear. |
| |
Altimeter |
Measures barometric pressure for scale
correction |
| |
Thermometer |
Measure temperature for scale
correction. |
| |
Extra survey Equipment: |
| |
Flags |
Do you have enough for your plan? |
| |
Flagging tape |
Could be useful. |
| |
Survey Record Form |
Are the information columns
adequate? |
| |
Clipboard |
|
| |
Pencils, ruler, protractor |
|
| |
Liscad Dongle |
Necessary to run the Liscad plotting
program. |
| |
Printer and paper |
Good for mapping and plotting
results |
| |
Cables |
Printer, laptop |
| |
Binoculars |
Helps to spot instrument or rod
person. |
| |
Walkie-Talkies |
Make sure batteries are fully charged and if
necessary have extras. |
| |
Calculator |
Useful for checking measurements and
calculations. |
| |
Metric grid paper |
Useful for checking plots and measurements,
and for mapping. |
| |
Rebar, steel rods, or stakes |
For benchmarks. You may also want
cement. |
| |
Sledge hammer |
Pounding benchmarks. You can use a rock
hammer, too. |
| |
Appropriate base map or topographic
map/airphoto |
Use these to locate benchmarks and reference
locations for the survey. |
Set-up
Choose an adequate instrument
station as described above. In detail, ensure that you can safely operate
the instrument without knocking it over. It is necessary to have the
center of the instrument, which is the point of intersection of the
transverse axis and the vertical axis of the instrument, directly over a
given point on the ground (the Instrument Station). Also, the circle and
the transverse axis must be horizontal (Moffitt, 1987). Remove the yellow
plastic cap from the tripod, and leave the instrument in the case until
the tripod is nearly level (see below). The tripod legs are spread (not
too vertical) and
their points are placed so that the tripod is approximately horizontal and
the telescope is at a convenient height for sighting (this is important:
you don't want to get a sore back from it being too low, nor do you want
to get sore calves and fall over from it being too high). The instrument
should be within 20 cm of the desired point, but no extra care is taken to
set it up closely at once. If the location of the instrument station is
not predetermined, set up first, and then use the optical plummet to
locate the benchmark: this will save time, because it takes extra care to
accurately set up over a benchmark. When setting up on rough ground, two
legs of the tripod should be set at about the same elevation and the top
of the tripod is made level by changing the length of the third. Consider
the common sighting direction and try to have one leg pointing that way so
that there will be a gap between two legs behind, and the instrument
operator will not have to straddle a tripod leg for the entire session.
If the instrument is more than a few inches from the given point, the
tripod is shifted bodily without changing the inclination of the legs and
it is set near as possible to the point. Check the level by placing a Brunton
compass on top of the tripod and adjusting gently until the Brunton bubble
level indicates that the top of the tripod is level. Tread tripod shoes
firmly into the ground, making sure to press along the leg and not
verically down (Anderson and Mikhail, 1989). If shoes do not penetrate to an equal depth,
re-level by extending or retracting the tripod legs. Before attaching the
instrument, check that the clamps of the telescopic legs are tight.
Once the tripod is nearly level and nearly above the desired point,
remove the Theodolite gently from its case and carry it with one hand on
the upper handle, and one hand below, to the top of the tripod, and
immediately screw the tripod fixing screw firmly into the bottom of the
theodolite. The levels on the instrument are very sensitive, and
therefore, the instrument should be completely set up in order to ensure
that it will be properly leveled. This will also give the tripod more
time to thermally equilibrate with the atmosphere and incident sunlight,
since differential thermal expansion of the tripod legs will effect the
levels.
Now you are ready for fine leveling of the instrument. Use the
three black footscrews on the tribrach (the device on the bottom of the
Theodolite to which the tripod fixing screw is attached) to center the
circular bubble. This is a coarse level. Turn the outer ring on the
eyepiece of the optical plummet until the crosshairs are in focus. Turn
the inner ring of the optical plummet until the ground point is in focus.
Slacken tripod fixing screw and move instrument over tripod plate until
cross hairs coincide with ground mark. Only translate the instrument over
the tripod plate, do not rotate it. Finally retighten fixing screw. Now do
the fine leveling.
Fine leveling instructions
1) Set plate level (the one in
the tube--this is the fine level) parallel to two footscrews. Center
plate level bubble by adjusting these two screws in equal and opposite
directions.
2) Turn Theodolite through 90°. Center bubble with third
footscrew.
3) Turn Theodolite through 180° (in the same direction as
above). Note position of bubble. Turn the third footscrew (same one used
in step 2) to bring the bubble to a point halfway between the position
noted and the centered position. Use the adjusting pin (in silver handle
in the Theodolite case) to turn the adjustment screw until bubble is
centered (see page 44 of the Theodolite manual for a picture).
4) Repeat until bubble remains centered within a single division for
any position.
Note that the instrument will drift out of
level as the day progresses. Repeat the above steps as needed and enter change
by pressing the level button (see
Operation). If the optical plummet is not above the ground point
desired, slacken tripod fixing screw and move instrument over tripod plate
until cross hairs coincide with ground mark. Only translate the
instrument over the tripod plate, do not rotate. Retighten fixing screw.
Now press the ON button and the startup menu will come on. Press the
white LEVEL (figure 1) key along the bottom of the key panel followed by continue. When the
levels are set press the continue button.
Now that the instrument is leveled up, set up and test the
electronics. First, insert the Verbatim SRAM card into the slot in the
Theodolite. Ensure that the arrow on the back of the card faces down when
you insert it. See below for a suggested initial key sequence for the
Theodolite and see the TPS-System 1000 Short Instructions System manual in
the Theodolite case for a list of commands for the Theodolite. The keypad
on the Theodolite allows for maximum utility with the minimum number of
keys. Therefore, most of the keys have several functions, depending upon
the class of operation. One way to remember the meaning is by noting the
background color of the keys.
Table 3. Classes of keypad operation for
Theodolite (TCM-1100) (Short Instruction Book) See Figure 2.
|
Class of operation |
Key color |
Example |
|
Fixed Keys |
White |
Functions which are always available. Returns to
last diologue. ON OFF. |
|
Function Keys |
Orange |
These keys correspond to the bottom line on the
display. Pressing SHIFT followed by an F key displays other
options. |
|
Navigation Keys
|
Green |
Vertical scrolling, position the cursor to edit,
insert or delete numerical data and characters, and position
colums. |
|
Numeric Keys |
Yellow |
1...9 Numerical input. ". " and +/- set decimal
place and sign. The Enter key to complete the data input of confirm a
selection out of a data list. Use the CE key to delete the last entered
digit or character. |
Figure 1. Keypad.
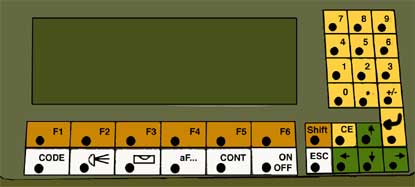
The ENTER button is important in that it executes the preceding
commands or answers in the affirmative, while the CE button often clears
the last command. Before anything, start with a fresh copy of the Survey
Record Form, and fill out the important details at the top. Use this form
to take notes while surveying. Remember to record all observations and
considerations, since the next time you look at this data, it might 6
months from now in the Dungeon! Record the observations so that someone
else can understand. After all, someone else might use the data.
Table 4. Suggested command sequence for
Theodolite start up
|
# |
Key sequence |
Description |
|
1 |

|
Switches Theodolite on. Screen briefly
displays software version.
|
2 |


|
After the bubble is level press the Continue
button. You can check and adjust level all day.
|
3 |

  
|
Select the setup file by pressing F5
(Setup) and using the arrows to select file. Press F6 to get the list of
files. Push enter to select (button with curved stem). It is also possible to set user templates based on many
different users or survey types with different needs.
We will go through the template setup later in the sequence. Press Continue to
go to the SETUP/ STATION DATA menu.
|
|
4 |
 x 4 x 4 |
Enter the station number (is it your first one of
the network?, or is it a new station setup within a network?). Use the down button
and enter instrument height. You measure this using the reflector staff and
holding it parallel with the station and up to the small hole (1 mm diameter) under the Leica
name on the right side of the Total Station. Arrow down and enter
station easting (we use 1000), station northing (we use 1000), and station
elevation (we use 100). Record this information on your Survey
Record Form. Make sure you are in meters, and if not, we will go through the
sequence below. |
|
5 |

 
|
Press F4 to enter in the reference azimuth. Point the instrument at the backsight or
reference azimuth and input the value. For example, 335.5 will set the reference
azimuth
and horizontal circle to 335.5°. All subsequent measurements will be
made relative to that direction. Record Hz0 on the Survey
Record Form. Press continue followed by F3, record. |
6 |

   
 |
Now you are back at the main menu. Press F4, Data, to see what
is in file. Scroll down with arrows to File, selct F6 to list files or F5 (search) to
examine individual files. By using the F3 and F4 keys, you can scroll through the
file history. Press Continue when finished.
|
|
7 |
     
|
You should be back at the main menu. Press F3 (CONF)
to system configuration. Press enter for user configuration. Press F4 (SET) if you need to change the
language or units. Press F6 to list the selections and enter to select it. We use ENGLISH, Metre, 3 Dec., 360
°, 3 Dec., °C, mbar, Easting/Northing, Clockwise (+), and V-drive left. Press CONT when
completed, and CONT to get back to main menu. |
8 |

 ( ( or or  ) ) 
 
|
We are going to set the user template. The first step is to set the recording mask.
From the main menu press F3 (CONF). Press Continue. From here you can change the recording mask sequence(F2) or the display mask (F3). Both are set in the following sequence: Press F6 (LIST) to
list the possibilites followed by the enter key to select and move to the next choice. When complete press CONT and set the
other mask if desired.
|
|
9 |
  
|
Now we are just about ready to shoot points. From Main Menu
press F6 (MEAS).
Enter the reflector height by pressing F4 (TARGET) and arrow down to Refl.Height and
enter in the reflector height in meters. Any time the reflector height changes it must be
changed in the Total Station and on the survey record form.
Record height on the Survey
Record Form.
Press CONT to save this change
and you will return to MEASURE MODE. For operation refer to chart E. |
Operation
Now that the instrument has been
set up physically and electronically, you are ready for operations.
Reflector
Check to make sure that the reflector
is properly mounted on the plumb pole by squeezing the small button on the
lower back portion of the reflector as you slip it down over the top of
the plumb pole. When you point the telescope at the reflector, the cross
hairs must intersect on the yellow reflector plate as shown in Figure 1.
This offset from the actual reflector is the same as the offset between
the center of the telescope and the EDM.
We also have a Triple Tilt Prism Assembly that is used for longer distances
.
Focusing and sighting
Focus the reticle cross hairs by
pointing the telescope at some other uniformly light surface (the sky),
and rotate the inner black portion of the eyepiece until the cross hairs
are sharp and black.
Point telescope toward reflector by means of optical sight. Use of
this sight will speed up acquisition of the reflector significantly. With
both eyes open, have the image of the white cross hair in the optical
sight in one eye, and the reflector in the other. When the two are
superimposed, you are approximately on target. This saves a significant
amount of time searching for the reflector with the actual telescope.
The horizontal and vertical rotations of the Theodolite are
controlled in two ways. First you can rotate the Theodolite horizontally by hand by
placing two hands on either side of it and rotating it. To rotate vertically, rotate
the EDM unit up or down by hand by nudging in up or down. Manual rotation works best
and is less demanding on the battery if there is a distance change from
point to point of several meters. Otherwise fine-tuning is done by
turning the horizontal and vertical knobs on the sides of the unit.
The instrument updates angle measurements within 0.3 seconds, so
the angles can be quickly displayed. In order to see the horizontal and
vertical angles of the current pointing, push  F2 (DIST). Before the station is moved press
F2 (DIST). Before the station is moved press  F3 (REC) to record the point.
F3 (REC) to record the point.
Measurement and recording
With the instrument pointed at the
reflector, ensure that the reflector operator is holding the reflector still and
level (by using the bubble level on the plumb pole), and then push F1 (ALL) . The EDM will measure the slope distance in about 3 seconds, and it will
display on the LCD of the EDM if you push
. The EDM will measure the slope distance in about 3 seconds, and it will
display on the LCD of the EDM if you push  (DIST).
Up to this point, the data has not been recorded. To record the
entire block of measured data, push
(DIST).
Up to this point, the data has not been recorded. To record the
entire block of measured data, push  (REC). If the format used is not the standard recording format (and
it is not if you followed the suggestion in step 8
above), the query
"
(REC). If the format used is not the standard recording format (and
it is not if you followed the suggestion in step 8
above), the query
"
OK?" appears on the
display before recording the first data block. Press OK to confirm and record the first data
block. This will happen each time the instrument is turned on. As you
can see, with many shots, you would end up pushing 
 often. To
make things go quicker, measurements that you don't want to check can be
speeded up by pushing
often. To
make things go quicker, measurements that you don't want to check can be
speeded up by pushing  . The
instrument will measure the distance and automatically record the block of
measured data and increment the current point number by 1. However, it
will not display the distance or other calculated values like Easting or
Northing in the LCD. To see these to check the shot, you would have to
press
. The
instrument will measure the distance and automatically record the block of
measured data and increment the current point number by 1. However, it
will not display the distance or other calculated values like Easting or
Northing in the LCD. To see these to check the shot, you would have to
press 
 (DATA)
(DATA)  (SEARCH) and then
(SEARCH) and then  to scroll
through the points.
to scroll
through the points.
As you are surveying it may be advantageous to switch operators
occasionally. Another important hint is to have simple hand signals to
communicate the status of the measurement to the reflector person or the type of topography to the
instrument person without
having to shout or use the two-way radios for simple communications (See
Communication techniques). I
like to have the instrument person hold his or her arm straight up when
starting to focus and measure to indicate to the reflector person that he
or she should hold the reflector level. As soon as the distance
measurement appears in the LCD, the instrument person's arm is held
sideways to indicate that the shot is complete and the reflector person
should move to the next target point. With this scheme, approximately
100 points per hour can be acquired. Our record for one day is 707 shots
with three people rotating through the two positions. If the target
points are further apart or in rough terrain, you may have two reflector
people, and alternate shots between them. This will speed up operations, but it requires more
coordination and concentration, especially on the part of the instrument
person.
Communication Techniques
Your surveying team may not be blessed with radio communication. However, there are some
basic arm signals that we have developed for geomorphic features.

|
"Shoot topo points."
|
|
"I'm ready to shoot point, please level the staff." |
 |
"End that series."
|
 |
"That was the first point for a linear feature (fault)."
|
 |
"That was the first point for a breakline." |
Coding specific points and breaklines
Coding specific points or breaklines adds
sort-of a dimentional
character to your map. We generally use the Total Station to produce
maps or profiles that contain features-such as
topographical breaks in slope-that, when accentuated with a polyline,
provide a three dimentional view on the map. This section will discuss
the coding system and cover the keypad procedure.
There are basically three types of codes: specific survey point codes
(i.e., landmarks),
polyline codes (i.e., topographic breaks), and physical feature codes (i.e., flotsam,
trees). Specific survey points, such
as a benchmark or survey mark are denoted by a symbol other than a dot.
Polylines connect a given set of points to denote a ridge, stream, scarp,
etc., and provide a line of which topolines will "break" along when plotted
using the Liscad software. Also, physical features such as vegetation,
roads, buildings, and electric can be symbolized on a map.
To assign a point or set of points to a code, first shoot the point as
described in Table 4, only make
sure to press F2  DIST. Next, you must set that point to
a code number.
DIST. Next, you must set that point to
a code number.
See this link for coding details: coding.
Data downloading, manipulation, and
software
I want to emphasize again the
importance of taking good notes while surveying. A few quick annotations
may save a major hassle down the road. Use the Survey Record Form to
organize the observations, and your organization and manipulation of the
data should go smoothly.
Data storage format
The memory card stores two types of information units: measurement
blocks and code blocks. With our present software set up, we don't use
code blocks. You are welcome to experiment with them. Other more
sophisticated software systems use the code blocks as part of the data
organization. The measurement blocks contain measured data and a point
number. Each block includes a consecutive unique block number which is
recorded automatically. If possible, record both the point number and
block number on the Survey Record Form in order to avoid ambiguity later.
The memory card data is made up of data blocks, each of which is
made up of words with a fixed length of 16 characters per word. Each
block may contain up to 8 words. A measurement block has the following
data format:
|
Word 1 |
Word 2 |
|
Word n |
|
|
Point number |
|
.... |
|
End character |
The first word of a measurement block always
contains the point number. The remaining words of the block are
determined by the measurement format of the Theodolite. Here is an actual
data block:
110001+00000000 21.103+09803900
22.103+08849970 31..00+00258533 51....+0100+000 81..00+00255904
82..00-00036142 83..00+00007194
While it appears quite cryptic, you can see
the word identifiers in there at the beginning of each word indicating the
data (
31 for example
is slope length). The first word, 110001+00000000, contains the
word identifier, 11,
meaning point number (click here for more codes; 21 is the horizontal angle, 22 is the vertical angle (measured from zenith, so that is why it is usually around 90 for the typical nearly horizontal shot0, 31 is the slope length, and 81, 82, and 83 are the easting, northing, and elevation respectively), then it is followed by the block number
(0001), and then the
point number (00000000). Each of these will be incremented automatically. The
running point number may be changed or input as surveying proceeds, but
the block numbers are unique. See coding for
corresponding features.
Downloading
The data should be downloaded from the SRAM card when the
surveying is complete. The SRAM card should then be cleared of data for
the next surveying trip. The Macintosh
computer systems that we use are not the type supported by the surveying
community; therefore, our scheme is original and somewhat circuitous, but
effective. In the motel, truck, or office, remove the SRAM card from the
Total Station, and insert it in the laptop. Open Microsoft Excel and open
file. Excel will ask you to choose from several options: plate 1- select
delimited; plate 2- select space and tap delimiters; plate 3- finish. All
your data will be in the form indicated below in the raw data block. This
form needs to be changed to either be viewed by Liscad or as northing,
easting, and elevation in excel.
Note that these days (2004), I typically just parse the raw file in excel and put a column break in on the left side of each plus as well as at the spaces, and then you can delete the columns you don't want and will have millimeters for the unit for the distances and easting, norrthing, and elevation which you can easily correct.
Filtering the data
Obviously the raw data is of little use for analysis.
Raw data block:
110549+00006000 21.323+07291800 22.323+09123700 31..00+00180854 81..10+01172836 82..10+01053110 83..10+00996292 87..10+00001300
410550+00000005 42....+00001101
|
Block # |
Point # |
Easting
E |
Northing
N |
Elevation
H |
Horiz. angle
Hz |
Vertical angle
V |
Slope length
D |
|
549 |
6000 |
117.2836 |
105.3110 |
99.6292 |
72.91800 |
91.23700 |
180.854 |
To view
as easting, northing, and elevation data in excel, you must first delete rows
that are not needed. The word identifiers (the first two numbers at the
beginning of the word) indicate the code of the word. We keep the point
number, 41 (point number), 42 (code), 81 (easting), 82 (northing), and 83 (elevation). Delete all other
columns. Be careful not to delete columns where additional data was
recorded causing a shift of words. You also need to add this to the header
(first line):
Wild REC-TotalStation
Here is a sample that works. It is important
to note that the data should be in this order because the program (liscad)
will take the second three words and assume that they are Easting,
Northing, and Elevation.
Wild REC-TotalStation
110549+00006000 81..10+01172836 82..10+01053110 83..10+00996292
410550+00000005 42....+00001101
110551+00006001 81..10+01177605 82..10+01046419 83..10+00992448
110552+00006002 81..10+01185919 82..10+01040090 83..10+00986772
110553+00006003 81..10+01193146 82..10+01036721 83..10+00985793
110554+00006004 81..10+01196477 82..10+01035305 83..10+00985896
110555+00006005 81..10+01211466 82..10+01026636 83..10+00979522
110556+00006006 81..10+01215893 82..10+01023119 83..10+00978902
110557+00006007 81..10+01221285 82..10+01019707 83..10+00977450
110558+00006008 81..10+01225470 82..10+01015623 83..10+00976024
110559+00006009 81..10+01240939 82..10+01016348 83..10+00975100
110560+00006010 81..10+01253217 82..10+01013742 83..10+00971985
110561+00006011 81..10+01271393 82..10+01012739 83..10+00969438
110562+00006012 81..10+01286564 82..10+01008193 83..10+00966146
110563+00006013 81..10+01290373 82..10+00997422 83..10+00964371
410564+00000005 42....+00000000
110565+00006014 81..10+01296148 82..10+00970876 83..10+00961116
110566+00006015 81..10+01302319 82..10+00944821 83..10+00958195
110567+00006016 81..10+01278370 82..10+00934876 83..10+00957227
110568+00006017 81..10+01272799 82..10+00954352 83..10+00959228
110569+00006018 81..10+01261752 82..10+00980963 83..10+00962315
110570+00006019 81..10+01265783 82..10+01001572 83..10+00965681
410571+00000005 42....+00002101
110572+00006020 81..10+01265783 82..10+01001563 83..10+00965681
110573+00006021 81..10+01253140 82..10+01001680 83..10+00966532
110574+00006022 81..10+01238534 82..10+00999553 83..10+00966963
|
110575+00006023 81..10+01250007 82..10+00944827 83..10+00957900
Lastly, save excel worksheet with a .ex
extension. This file will be the master archive for your data. From it
you can manipulate, plot, and contour your data. Print this file out and
save the hardcopy somewhere safe.
Care
Our surveying equipment is fairly
rugged and designed to last. However, it is also expensive and likes a
little attention and Tender Loving Care occasionally. Giving the
equipment a good cleaning occasionally and treating it with care will
ensure that it will last for a long time. Here are some basic
suggestions.
Transport
For transport, use shockproof
packaging material for the instruments. We have nice carrying cases for
the EDM and Total Station and most of the associated hardware. While these
cases add significant weight, they really do protect the instruments, and
the one time that you decide to lighten your load and only carry the
instruments, will be the one time that they fall down a hill and are
severely damaged--a fall which they would have survived had they been in
the cases!
Cleaning and drying
Before cleaning, blow dust off lenses
and prisms. Handle lenses, eyepieces and prisms with special care.
Always use a soft, clean cloth or clean cottonwool. Breathe on glass
components, then wipe gently. If necessary, slightly moisten cloth or
cottonwool with pure alcohol. Do not use any other liquid. Never touch
optical glass with your fingers.
Cables and plugs
Clean periodically. Do not let plugs
get dirty. Protect from moisture. Use pure alcohol to rinse dirty cable
connectors, then leave to dry thoroughly.
Condensation on prisms
When a prism is cooler than the
ambient air it may collect condensation. If this happens, warm the prism
for some time by placing it in a warm environment (room, vehicle, or
inside clothing). Merely wiping the prism is useless.
Storage
If an instrument has become wet,
unpack it on return to base. Carefully clean the instrument, accessories,
case and foam inserts. Wipe dry. Repack only after all the equipment is
again thoroughly dry.
In the field
The main perils in the field to the
instrument are rain, blowing sand, heat, and being knocked over. If it is
raining or blowing hard, you will have to postpone the effort. Protect
against light mist and moderately blowing sand by placing one of the
plastic hoods (stored in the EDM case) over the instrument whenever it
will not be used for longer than several minutes. If the temperature is
less than -20°C or greater than +50 °C, you should not operate
the instrument. Protect against temperature fluctuation with an
umbrella. Walk carefully when working around the instrument and when
setting up, check to make sure that the area is clear of debris that may
be an obstacle.
How it works
Electromagnetic Distance Measurement (EDM)
One of the fundamental measurements
in surveying is distance. Obviously with a distance and an angle, one can
establish a coordinate system and locate the relative positions of objects
or observations. The angle defines the orientation and the distance of the
scale. The direct measurement of distance in the field is one of the more
troublesome of surveying operations, especially if a high degree of
accuracy is desired. Indirect measurements, like the use of a stadia rod,
have been developed and used extensively; however, these systems are of
rather limited range and accuracy. With the advent of electromagnetic
instruments, the direct measurement of distance with high precision is
possible (Burnside, 1991).
When a distance is measured using an EDM instrument, some form of
electromagnetic wave (in our case, infra-red--IR--radiation) is
transmitted from the instrument towards a reflector where part of the
transmitted wave is returned to the instrument. Electronic comparison of
the transmitted and received signals allows for computation of the
distance (Price, 1989). See Figure 3 for a schematic of the method of
operation of an EDM.
Figure 3.1 Schematics of EDM system. From Price and Uren,
1989.
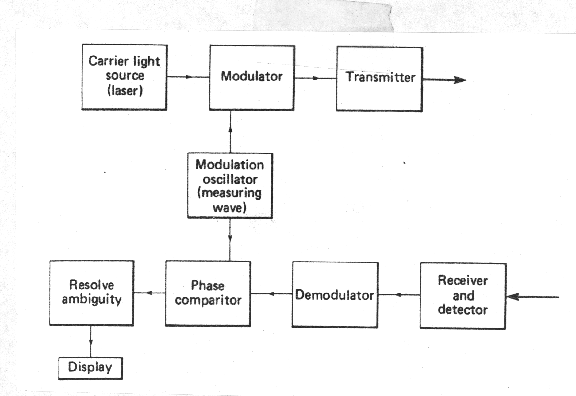
Electromagnetic waves
Electromagnetic waves can be represented by a sinusoidal wave
motion. The number of times in 1 second that a wave completes a cycle is
called the frequency (f), and is measured in
Hz. The length of one cycle is called the wavelength (
l), which can be determined as a
function of the frequency from
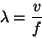 (1)
(1)
where v is the speed of propagation of the wave.
The speed of electromagnetic waves in a vacuum is called the speed
of light, c, and is taken to be 299,792,458 m s
-1.(Price, 1989). The
accuracy of an EDM instrument depends ultimately on the accuracy of the
estimated velocity of the electromagnetic wave through the atmosphere
(Burnside, 1991).
A relationship expressing the instantaneous amplitude of a
sinusoidal wave is
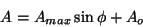 (2)
(2)
where A
max is the maximum amplitude developed by the source,
A0 is
the reference amplitude, and f is the phase angle which completes a cycle in 2╣ radians or
360°.
In an EDM system, distance is measured by the difference in phase
angle between the transmitted and received versions of a sinusoidal wave.
The double path length (2D) between instrument and reflector is the
distance covered by the radiation from an EDM measurement. It can be
represented in terms of the wavelength of the measuring unit:
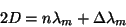 2 (3)
2 (3)
The distance from instrument to reflector is D,
lm is the wavelength of the measuring unit, n is the
integer number of wavelengths traveled by the wave, and Dlm is the fraction of the wavelength traveled by the wave.
Therefore, the distance D is made of two separate elements. An EDM
instrument using continuous electromagnetic waves can only determine
Dlm by phase comparison (Figure 4).
If the phase angle of the transmitted wave measured at the
instrument is
f1, and the phase angle measured on
receipt is f2, then
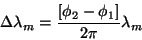 (4)
(4)
The phase angle
f2 can apply to any incoming wavelength,
so phase comparison will only provide a determination of the fraction of a
wavelength traveled by the wave, leaving the total number, n,
ambiguous (Price, 1989).
Figure 4. Phase comparison. (a) An EDM is set up at A and a reflector at B for determination of the slope length (D). During measurement, an electromagnetic wave is continuously transmitted from A towards B where it is reflected back to A. (b) The electromagnetic wave path from A to B has been shown, and for clarity, the same sequence is shown in (c), but the return wave has ben opened out. Points A and A' are effectively the same, since the transmitter and receiver would eb side by side in the same unit at A. The lowermost portion also isslustrates the ideal of modulation of the carrier wave by the measuring wave. From Price and Uren, 1989.
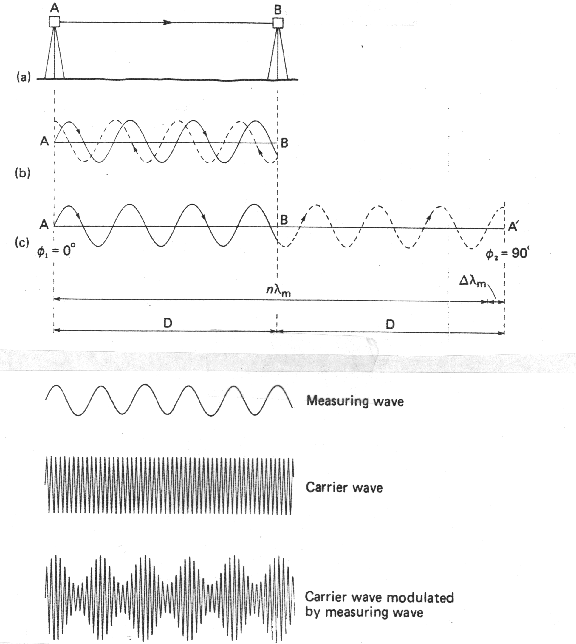
For many EDM instruments, an accuracy in measurement between 1 and
10 mm is specified at short ranges, and a phase resolution of 1 in 10,000
is normal. Assuming an accuracy of at least 1 mm, therefore, a measuring
wavelength (
lm) of 10 m is required. Approximating
the speed of propagation, v, by 3 x 108 m s-1, 10 m corresponds to a frequency of 30
MHz. Adequate propagation of an electromagnetic signal of 30 MHz
frequency for EDM purposes is not practical, so a higher frequency carrier
wave is used and modulated by the measuring wave (Figure 5, (Price,
1989)). In the case of our instrument, the carrier wave is infra-red,
with a wavelength of 0.835 Ám, corresponding to a frequency of 3.6 x
105 GHz.
The return signal is usually amplified, and then the phase
difference is determined digitally. The signal derived from the
modulation triggers off the counting mechanism every time the signal
changes from negative to positive. The signal derived from the reflected
ray stops the counting mechanism (Burnside, 1991). For our instrument,
the integer ambiguity (n) of wavelengths is determined using the
coarse measurement frequency of 74,927 Hz, equivalent to 2000 m, and the
amplitude modulation of 4,870,255 Hz (30.7692 m) provides the fine
measurement (
Dlm). In order to achieve the stated
accuracy of 5 mm, the phase measurements are accurate to 1 part in 6,154.
Errors in distance measurement
The path of electromagnetic energy is the true distance that is
measured by the EDM, and will be determined by the variability in the
refractive index through the atmosphere.
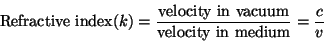 (5)
(5)
Since the medium is air, the velocity is nearly the same as that of a
vacuum, and so the refractive index is nearly one, and for standard
conditions may be taken to be 1.000320. The exact value of the refractive
index is dependent on the atmospheric conditions of temperature, pressure,
water vapor pressure, frequency of the radiated signal, and composition.
Therefore, for measurements of the highest accuracy, adequate atmospheric
observations must be made. Other potential error sources are from path
curvature (similar to the curvature of the earth).(Burnside,
1991).
Scale error
One source of error that is adjusted for in our instrument is a
scale correction in units of ppm that adjusts for slight errors in the
reference frequency and in the accuracy of the average group refractive
index along the line of measurement. The ppm value is set to 0 on the
EDM, and adjusted in the theodolite.
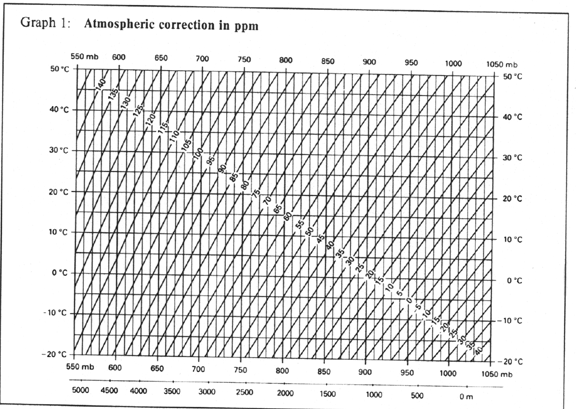
Atmospheric correction is one scale error adjustment that takes
into account both atmospheric pressure and temperature. It is an absolute
correction for the true velocity of propagation, and not a relative scale
correction like reduction to sea level (see below). To determine the
atmospheric correction to an accuracy of 1 ppm, measure the ambient
temperature to an accuracy of 1°C and atmospheric pressure to 3 mb.
For most applications, and approximate value for the atmospheric
correction (within about 10 ppm) is adequate. This can be obtained by
taking the average temperature for the day and the height above mean sea
level of the survey site. A temperature change of about 10°C or a
change in height above sea level of about 350 m (= 35 mb) varies the scale
correction by only 10 ppm. The atmospheric correction is computed in
accordance with the following formula:
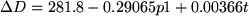 (6)
(6)
where:
DD1 = atmospheric correction (ppm), p = atmospheric
pressure (mb), and t = ambient temperature (°C). For extreme
conditions of 30°C temperature change and 100 mb pressure change, one
can expect variations in scale error of 50 ppm in a day. This maximum
value is ten times greater than the stated initial accuracy of the
instrument, and therefore should be accounted for by adjusting the scale
error on the theodolite occasionally during the day's surveying effort
(see Figure 6, graph 1 to determine DD1).
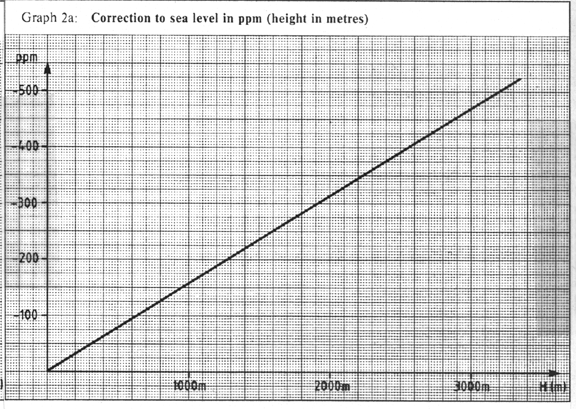
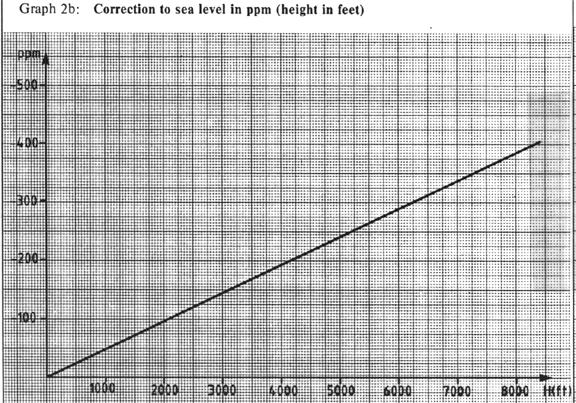
The correction in ppm for the reduction to mean sea level is based
upon the formula:
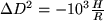 (7)
(7)
where
DD2 = reduction to MSL in ppm, H = height of EDM above
MSL, and R = 6378 km (earth radius). This correction is a
constant and should be determined at the beginning of the survey effort by
consulting Figure 6, graph 2a or 2b.
Corrections in ppm may be made for map projections as well.
Reduction formula
The theodolite computes slope distance according to the following
formula:
D = D0x(1+deltaDx10-6) + mm
where D is the corrected slope distance in mm,
D
0
is
the measured (uncorrected) slope distance in mm, (deltaD) 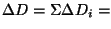 = sum of scale corrections (n is the number of scale
corrections) in ppm, and mm = prism constant in mm.
= sum of scale corrections (n is the number of scale
corrections) in ppm, and mm = prism constant in mm.
The theodolite computes horizontal distance (D
h) and height difference
(eh) by
accounting for earth curvature and mean refractive index. These
corrections are on the order of 10-8 or 0.01 ppm of D0 and therefore not
significant compared to the scale correction (~50 to 100 ppm).
Figure 6. Scale correction graphs from Theodolite manual. Use these
to determine
DD (sum of scale corrections).
Infra-red radiation from a GaAs lasing diode
The source of the IR radiation for our instrument is a Gallium
Arsenide (GaAs) lasing diode. This device is made from a small chip of
semiconducting material, and is similar in size and appearance to other
semiconducting devices (Figure 7). Driven by a forward biased voltage and
maintained by different electrostatic potentials in the two halves of the
diode, an electron population inversion between the two halves of the
diode will provide the energy level transition for stimulated emission of
photons by electrons as they fall to the lower energy state (Price,
1989). The energy difference is emitted as radiation (and thus the
process and device are called a laser--Light Amplification by the
Stimulated Emission of Radiation). The process of stimulated emission
enables the laser to emit an intense, monochromatic radiation that travels
as a narrow beam for considerable distances before it spreads out (Price,
1989). The intensity of the IR radiation is nearly linearly proportional
to the current flow and with virtually an instantaneous response
(Burnside, 1991). If an alternating voltage is superimposed upon the
normal operating voltage of the GaAs diode, the intensity of its emitted
radiation varies in sympathy with the alternating voltage (Figure 8,
Price, 1989). This provides a simple and inexpensive means of directly
modulating the infra-red beam.
The GaAs diode is widely used in surveying. The small dimensions
of the junction in which the radiation is emitted gives rise to poorer
collimation of the radiation. Therefore, the GaAs laser emits a beam with
a relatively large elliptical spread and the brightness of the GaAs laser
is lower than that of other lasers. The spectral width of the radiation
emitted is usually 2-3 nm compared with 0.001 nm of the visible light,
HeNe gas laser and thus the GaAs laser lacks the monochromacity of other
lasers, contributing error to the effective propagation velocity.
However, GaAs lasers can be made to operate at orders of magnitude greater
efficiency than other lasers, can be made much smaller and more rugged,
and are considerably less expensive than other lasers (Price, 1989).
Because of the relatively low power radiated, a beam of sufficient
power will not be reflected from an unprepared surface. A special
reflector is therefore used in order to ensure a good return signal. A
plane mirror can be employed, but it requires accurate setting, so in
practice, a corner cube reflector is most often used. This reflector will
return a beam along a path parallel to the incident path over a wide range
of angles of incidence onto the front surface. A cube of glass is usually
used with its edges ground into a corner with accuracies of grinding to
within a few degrees of arc (Burnside, 1991). The path length of the
signal within the reflector must be corrected for, and that is the reason
for the setting of the prism constant within the theodolite. The constant
for Wild circular prisms is 0. Note that over short distances, the
"cat-eye" type reflector commonly used for bicycles will adequately
reflect highly oblique incident signals.
Figure 7. Gallium arsenide diode characteristics. From Burnside, 1991.
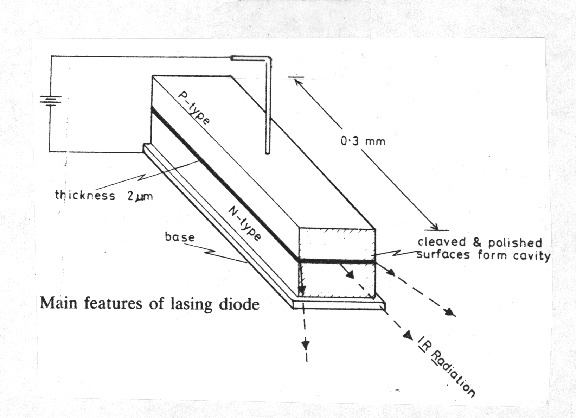
Figure 8. Modulation of a Gallium arsenide diode. From Price and Uren, 1989.

Selected Technical Data--Leica (Wild)
DI4L
|
Standard deviation of distance
measurement |
5 mm + 5 mm/km |
|
Breaks in beam |
result not affected |
|
Range with one reflector |
1.2 km in strong haze
2.5 km in average atmospheric conditions
(the maximum range I have shot is 1.8 km) |
|
Carrier wavelength |
0.835 Ám infra-red |
|
Fine measurement |
4,870,255 Hz = 30.7692 m |
|
Coarse measurement |
74,927 Hz = 2000 m |
|
Weight--DI4L
Counterweight
Container
Total weight |
1.1 kg (2.4 lb)
0.8 kg (2.0 lb)
3.8 kg (8.4 lb)
5.7 kg (12.8 lb) |
|
Beam width at half power |
4' (12 cm at 100 m) |
Theodolite
The Theodolite is an accurate
horizontal and vertical angle measuring device with a telescope and on
board electronics for data storage and EDM operation. Fortunately for us,
the angles are measured and recorded accurately and electronically,
avoiding the need for us to read a vernier and record data manually as is
typical on transits and optical theodolites. This electronic theodolite
contains circular encoders which sense the rotations of the vertical and
horizontal spindles of the telescope, and converts those rotations into
horizontal and vertical angles electronically, and displays the values of
the angles on a Liquid Crystal Display (LCD) (Moffitt, 1987).
The integrated EDM/Theodolite combination is often called a "Total
Station" or "Total Geodetic Station." Output from the horizontal and
vertical circular encoders and from the EDM are stored in a data
collector. The instrument may convert the data (horizontal and vertical
angles and the slope distance) electronically into Easting and Northing
coordinates, height difference, and horizontal distance (Moffitt,
1987).
Selected Technical Data--Leica (Wild
T-1000)
|
Standard deviation of angular measurement
|
3.0' (seconds of a degree) horizontal and
vertical |
|
Telescope |
Erect image |
|
Magnification
|
30x |
|
Shortest focusing range
|
1.7 m |
|
Field at 1000 m
|
27 m |
|
Displays |
2 LCD displays each for 8 digits, sign,
decimal point and symbols for user guidance |
|
Keyboard |
Weatherproof, 14 multiple function keys,
contact pressure 30 g |
|
Automatic power off |
About 3 minutes after last
keystroke |
|
Angle measurement |
Continuous, by absolute encoder |
|
Updates
|
0.1 to 0.3 seconds |
|
Optical plummet (in tribrach) |
Focusing |
|
Magnification
|
2x |
|
Temperature Range |
-20°C to +50°C |
|
Weight--T1000 |
4.5 kg (9.9 lb) |
|
Container
|
3.9 kg (8.6 lb) |
|
Total weight |
8.4 kg (18.5 lb) |
Determination of Easting, Northing, and
Elevation
The actual observations made by the
Total Station are the horizontal and vertical angles (Hz and
V), and the slope length (D)--these are called fundamental
measurements. Clearly, from these data, one can determine the relative
coordinates of the instrument and reflector (Figure 9). The instrument
makes its own reductions based only upon the fundamental measurements.
The horizontal angles are made relative to a backsight or reference
azimuth or known orientation. This may be determined by a careful compass
sighting to a distant, but stable and easily identifiable landmark, or it
may be arbitrary. Once the backsight is made, the reference azimuth,
(hz0) may be set on the Theodolite. The vertical angle may
be called a zenith angle and is measured in a vertical plane down from the
upward direction of a vertical or plumb line (Moffitt, 1987).
Instrument Station Reference Location
The point over which the Total Station is set up is called an
instrument station. Such a point should be marked as accurately as
possibly on some firm object. On many surveys, each station is marked by
a wooden stake, spike, or piece of REBAR driven flush with the ground and
into the top of which a small (~ mm diameter) dimple is marked (a tack may
be put in the wooden stake) (Moffitt, 1987). The Total Station
measurements and reductions are made relative to the instrument station
(E
0,
N0, and
H0--where E refers to distance East, N distance
North, and H elevation, and the subscript 0 indicates a reference value). These
values must be predetermined by other means (triangulation, previous
survey location, Global Positioning System, etc., or they may be
arbitrary). In fact, for most local surveys, with only one survey set up,
the instrument station is commonly taken to be (0, 0, 0).
Determinations in the vertical plane
In the lower portion of Figure 9, the geometric reductions in a
vertical plane are indicated. From the fundamental measurements and a few
more observations, the horizontal distance (HD) and elevation
(H) may be determined:

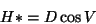
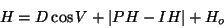 (9)
(9)
H* is the elevation difference between instrument and reflector,
IH is instrument Height, and PH is the Prism Height.
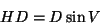 (10)
(10)
Figure 9. Surveying geometry.
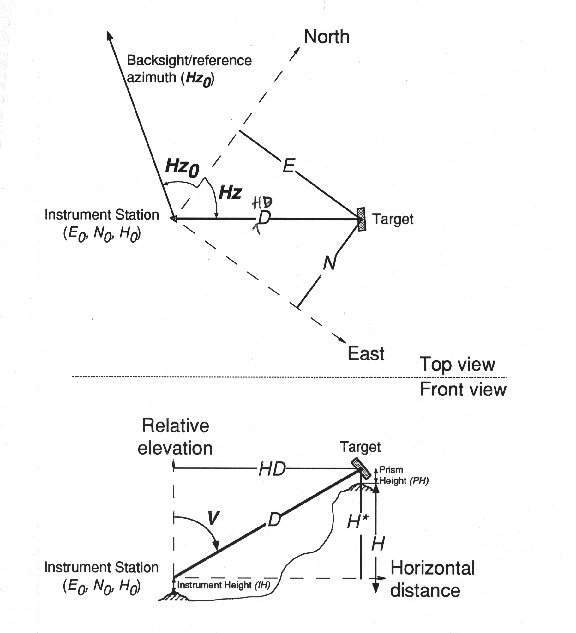
Determinations in the horizontal plane
In the upper portion of Figure 9, the map view reductions from the
fundamental measurements are shown. Because we are interested in the map
relations of the surveyed objects or observations, the distances East
(E) and North (N) may be determined in the following way:
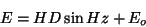 (11)
(11)
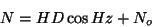 (12)
(12)
Foresight and Backsight: the traverse
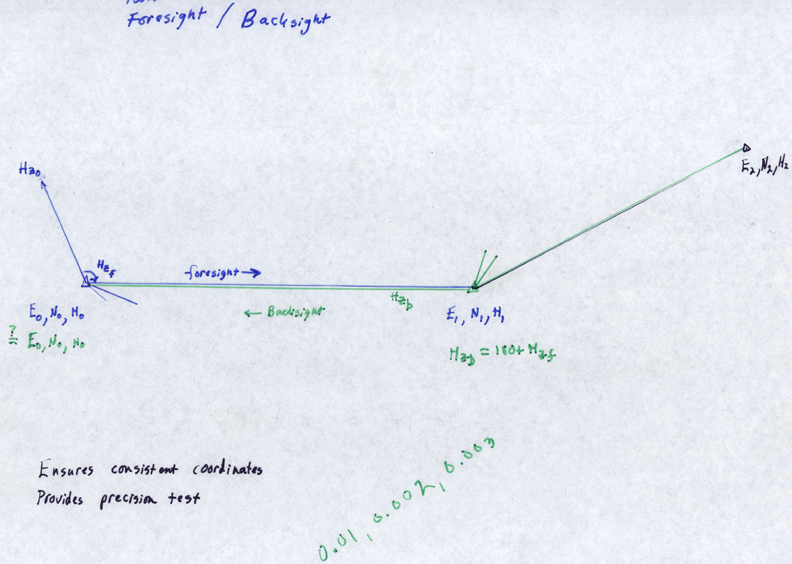
One other thing that people have trouble with and that I have only recently gotten to the bottom of is the traverse or how you move your station to a new position. The figure below shows how one starts of at the reference position E0, N0, H0, works, and then moves to the new station with a reference position E1, N1, H1. What you have to do is shoot from the first location to the second (foresight) and record the E1, N1, H1, and the bearing Hz0. Then, move to the new location, set up, tell the total station you are at E1, N1, H1, and set the horizontal circle to Hz1 or Hz0+180 degrees (backsight). Then shoot to the reflector set up at the first station and record the position. It should be within a few mm of the original E0, N0, H0.
Precision
The angular accuracy at one standard
deviation of the Theodolite is 3", and the linear accuracy at one standard
deviation of the EDM is 5 mm ▒ 5 ppm of the slope length. The upper
portion of Figure 10 shows a map view of the 1 standard deviation error
volume (remember that the horizontal and vertical angles have the same
precision). In reality, this volume is really an ellipsoid if we assume
that the errors are normally distributed. The significance of this figure
and the plot in the lower portion of Figure 10 is that one can anticipate
the precision and its changes with slope length, and consider them
accordingly. For example, for a 100 m shot, or slope length D =
100 m, the linear error, l, is 5.5 mm, and the angular error, a, is 1.5
mm, and therefore, the error volume is 11 mm along the shot, and 3 mm wide
along horizontal and vertical arcs. Note that this is much smaller than reflector placement error.
Planning and executing a
surveying/mapping project
The important concern when
planning a mapping project is the question that is being asked, or problem
being addressed. While mapping and surveying may be intrinsically
fascinating and interesting of themselves, unless you want to become a
surveyor, they are only methods used to collect data in order to address a
geologic problem. Therefore, the technique and methods should be
appropriate for the problem. You should collect data at the appropriate
scale and precision that will most efficiently shed light upon the
problem. Check (Compton, 1985) for an inspiring and essential text to
guide you in the field.
Basic detailed mapping procedure
This technique is appropriate for
outcrop to kilometer scale mapping (1:10 to 1:1000 scale) for which no
adequate base map exists. The basic idea is to shoot in control points
with the Total Station, establish a base map, and then use tape and
compass and triangulation to interpolate and locate features between the
control points.
Figure 10. Surveying precision.

1) Recon the area. Consider the problem, and instrument locations.
2) Flag points. Place flags (numbered) on important features (along
large fractures or contacts for example). The density depends upon the
scale of the problem and the map. If the flags are too close, you will
spend a long time shooting them in and then may be confused while
mapping. If they are too far apart, you will spend a long time measuring
off distances and bearings between points. I suggest a radial distance
between flags of 5 to 10 m.
3) Shoot points with Total Station. Make sure that the point number
corresponds either directly or in some noted way with the flag numbers.
4) Produce basemap. This may be done in several ways. It may be done
in the field or the office by manually plotting the location and recording
the elevation of the point on grid paper. Be sure to use metric grid
paper. The other way to produce the basemap is to download the data as
described above, and contour and plot the points with their numbers.
Print the contour map out to an appropriate size for your mapping. I do
this step in Deltagraph Pro by importing a four column (point number, E,
N, H) Excel file, and then plot an XYZContour chart (select the data by
using the arrow in between the two label words:
Show symbols, and adjust the size of the chart by
selecting Axis Attributes under the Axis choice under the Chart menu.
Make sure that the X and Y (E and N) axes are the same scale. Choose an
appropriate contour interval. Show the labels of the points (point
numbers, for example) by selecting the chart, and then under the Chart
menu, select Show Values, and choose a location besides None, and the Text
should be Category. This will plot the items in the corresponding cell in
the Labels Column adjacent to the symbol.
5) Mapping. The above method should provide a basemap with the control
points displayed and labeled. Tape the base map or a portion of it to
your map board and overlay a piece of vellum or mylar. Mark the control
points and a few more index marks, especially if you will use more than
one page for the base map. As you map, observe the locations and
orientations of objects and features by noting the bearing and distance
(using a Brunton Compass and a tape measure or a well calibrated pace)
from one or more control points. You may also shoot a bearing to two or
more control points, plot the angle on the map and triangulate your
location. Mark your observations carefully with a sharp pencil. As you
map, record the topography. If you plotted contour lines, trace and
modify them in the field and include the subtleties that you can. In the
evenings or whenever you are at a stable point, trace your lines in ink
using a very fine pen.
Examples
Below are a few examples of
different mapping projects our members of our group have completed
recently. These are meant to illustrate the different solutions to
different problems that have been achieved.
Topography
My own interest in the geomorphic
responses to active faulting provides the following example. During the
June 28, 1993 Landers California earthquake, spectacular faulted landforms
were produced all along the surface rupture. These landforms provided an
important opportunity to document the original shapes and initial
modification of faulted landforms. This project posed several interesting
survey challenges: 1) producing detailed scarp profiles and longitudinal
profiles of gully main and tributary channels, and detailed topographic
contour maps of faulted knickpoints; 2) establishing a cheap but
hopefully stable control network; and 3) reoccupying the network.
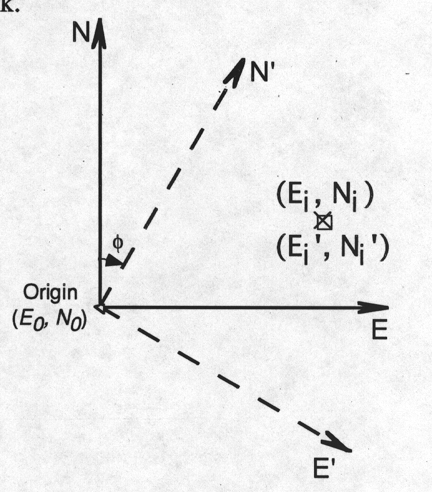
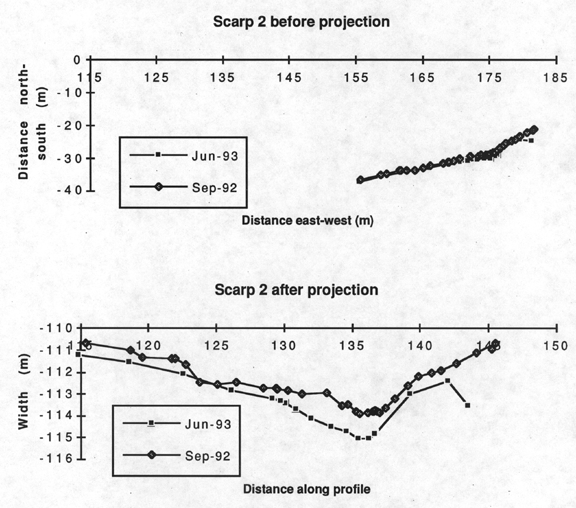
Scarp profiles--coordinate transformation by rotation
These profiles are made perpendicular to the fault scarp and
are ideally planar. In the field, we marked the upper and lower ends of
the profiles with steel rods, and walk between, shooting points about
every 50 cm until we are at the free face of the scarp, where points are
shot about every 10 - 20 cm. These data are down loaded as described
above, and then the profile is projected to a plane perpendicular to the
scarp. The coordinates are transformed by a rotation about the origin so
that one axis is the distance along the profile and the other is the
deviation from the plane of the profile. The equations for such a
coordinate transformation are as follows:
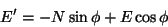 (13)
(13)
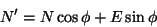 (14)
(14)
The figure above and to the right illustrates
this geometry.
The following two figures illustrate the initial and rotated coordinate
systems for a scarp profile. In the lower plot, the coordinate system has
been rotated by -36° (counterclockwise), and the horizontal axis used
as the horizontal distance along the profile. The vertical axis indicates
that the deviation from a plane is a maximum of 5 m over 30 m.
Longitudinal profiles
The gully longitudinal profiles were determined by observing
points along the lowest portion of the active channel in a given gully.
The distance along the profile is the sum of the distances between
individual points. In other words, the longitudinal profile is not
projected to a plane, rather the run, or distance along the
channel, is stretched out and plotted as the horizontal axis for the
longitudinal profile, while the vertical axis is the corresponding
elevation measurements. This plot is important since it indicates the
effective slope for the flow, which clearly may not be ideally contained
within a single plane.
Contour maps - topographic mapping
Because of the precision and rapidity of data acquisition of
our Total Station, as well as the opportunity to quantitatively document
the three-dimensional (i.e. volumetric) changes in scarp form,
particularly where the gully channels were disrupted by the earthquake
surface rupture, we made detailed observations of small portions of the
gully channel surfaces. We have observed after one year, and expect
significant change within a few years. The data were observed over a
relatively small area (125 to 250 m
2) at a fairly high density: 1
measurement every 0.5 to 2.5 m2. The lower density shots seemed to
optimally address the problem, and we achieved them by setting a goal of
100 shots to complete the map. This seems to be a better psychological
tactic than simply observing every apparently important break in slope.
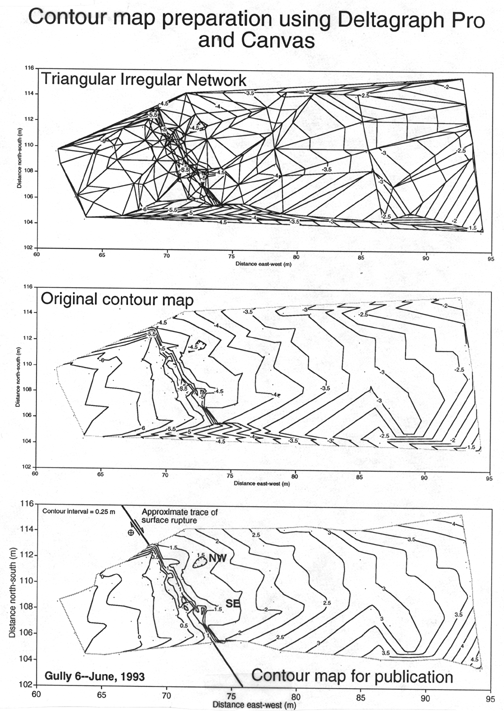
We used the program Deltagraph Pro to contour our data. This
program has two advantages: 1) it can contour a set of data with an
irregular boundary, enclosing the area of interest with a relatively close
fitting polygon, instead of a rectangle, as is common with most contouring
programs; and 2) it uses triangle-based terrain modeling (commonly called
a Triangular Irregular Network--TIN; Kennie, 1990). This method
essentially models the surface as a series of planar, triangular elements,
each of which contains three neighboring data points (Figure 11). As you
are surveying it is important for the reflector person to attempt to
visualize this triangle network in order to assess the appropriateness of
a given observation point. The points where contour lines intersect the
lines between neighboring points are determined by direct, linear
interpolation. The contour lines are then determined by connecting those
intersections. Because the contour lines are not smoothed, this method
provides a basic contour map that honors each data point directly.
However, it does generate a somewhat jagged map which incidentally appears
more appropriate for semi-arid landscapes rather than smoother
humid-temperate landscapes.
Given a method of plotting the map and taking it in the field, the
subtleties of the contours could be adjusted manually. We adjusted our
maps slightly in the office, honoring the topography as best as possible,
by adding a few more vertices to the contour lines in the drawing program
Canvas (Figure 11).
Figure 11. Contour map preparation using Deltagraph Pro and Canvas.
Reoccupation
There are three types of errors:
random errors, systematic errors, and blunders (Kennie, 1990). Random
errors result from the random normally distributed probability of a
measurement. Systematic errors cannot be detected by redundant
measurements because they effect all measurements similarly. However,
they can be addressed by making more observations; for example the scale
error due to atmospheric changes that is explained above is a type of
systematic error that can be minimized by making observations of
temperature and pressure and making the appropriate scale adjustment.
Blunders are human errors that hopefully are minimized or large enough to
be noticed and removed from the data.
Errors within a single survey are rather small. Reoccupation of a
survey network in order to repeat measurements may be desirable, but it
incorporates greater error. The best way to adjust two sets of data
measured of the same network during successive occupations of a survey
network is by least squares. In this technique, the squares of the
residuals of the observations are minimized:
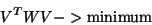 (15)
(15)
where V = l
i’ - li, in which li is the observation and
li’ is the
adjusted observation, and W is a weight matrix consisting of the
inverse of the covariance matrix of the observations. If the data are not
correlated, the matrix will be diagonal, and if the variances of all the
data are the same, the W matrix may be dropped from the
determination (Kennie, 1990).
Detailed Fracture Mapping
Finally, as an example of the mapping
technique I described above, I will briefly discuss the method by which we
made a detailed fracture map of a portion of the surface rupture of the
Landers earthquake (Antonellini, 1992). See Figures 12 and 13. First, we made a reconnaissance
of the area, and noted the important features and discussed the problem
and the pertinent observations. Second, we determined the approximate
size: ~700 m long by ~250 m wide. We considered the mapping scale by
determining the basemap size for various mapping scales: 1:250--the
ultimate scale chosen--would result in a basemap approximately 2.8 by 1 m
in size. We divided into four mapping groups, so each would have a base
map approximately 0.7 by 1 m--probably the maximum comfortable size for a
single sheet. Third, we flagged numbered control points along fractures
and other obvious and important features. Fourth, the southeastern third
of the control points were located using a conventional plane table set
up. The northwestern two-thirds of the control points were located using
the Total Station in approximately the same time as that for those done
with the plane table. We did not have a means of automatically plotting
our data in the field, so we did it manually. Here we made things
difficult by having grid paper ruled in English units: inches and ten
divisions. This made it necessary to convert the measurement read off of
the Total Station LCD in metric units to the quirky and irregular English
scale. With metric ruled paper, and such a regular mapping scale of
1:250, it would have been much easier to lay off the base map control
points. The points were plotted with the point number and
elevation adjacent to the symbol, and then four basemaps generated by
overlaying sheets of mylar on the control point map, marking the control
points (including some shared by the adjacent maps to help with future
compilation). With the control points marked in pen on the basemaps, we
were ready to do our mapping of the surface fracturing. Each mapping
group had a measuring tape and compass, and recorded observations relative
to the control points within the mapping area (Figure 12). As mapping
proceeded, topography was recorded, and contours generated. The contours
generated varied in their precision depending upon the effort of the
mappers. The most successful contour generation technique was for one
member of the mapping group to put his eye level at the level of a contour
and site along a level line determined by the Brunton compass toward the
landscape, and the contour continued and mapped in by communication with
the mapping partner who interpolated between the control points in a
manner similar to that used for mapping other features (Cooke and
Christiansen, Figure 12). As mapping progressed, observations and contour
lines were inked. The final map was compiled and drafted by Ken
Cruikshank (Figure 13). It was presented at the Fall, 1992 AGU meeting
(Antonellini, 1992).
Figure 12. Reduced portions of original basemaps from landers earthquake surface rupture mapping (Antonellini and others, 1992). Note the different styles and representations of fractures, topography, landforms, and human impacts.
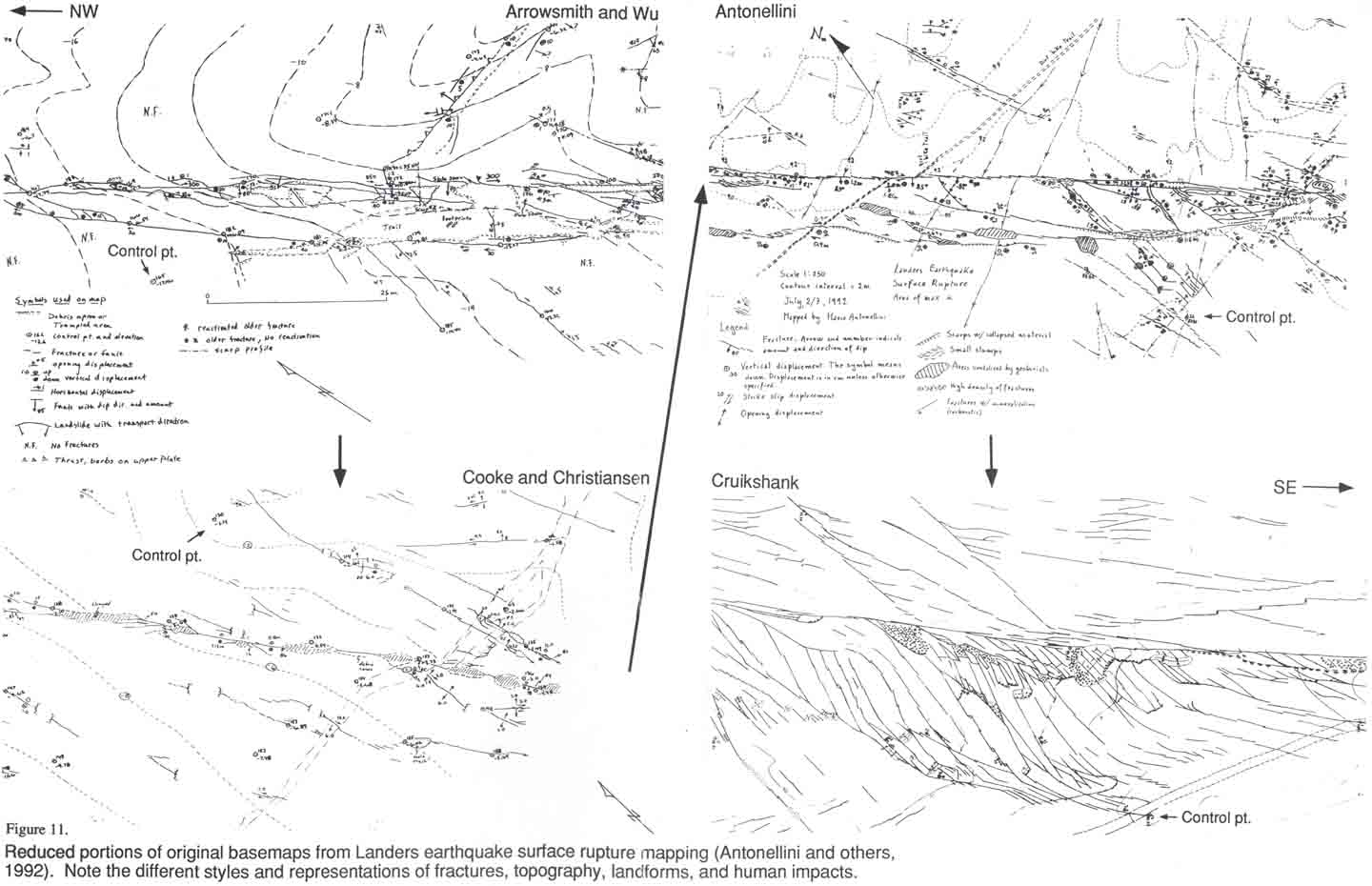
Figure 13. Final analytical fracture map from Landers study (compiled by Ken Cruikshank)..

Bibliography
Geologic mapping
Compton, R. R., 1985, Geology in
the Field: New York, John Wiley and Sons, 398 p.
The best field geology book available. Covers all of the basics
from rock identification through basic outcrop procedures to aerial
photography. You should own it.
Electromagnetic distance
measurement
Burnside, C. D., 1991,
Electromagnetic distance measurement: Boston, Blackwell Scientific
Publications, 278 p.
Good reference on the subject. A bit arcane in the explanation of
the basics, but thorough. Includes a nice description of different
equipment (3rd edition, TA601.B87 1991, Engineering Library).
Price, W. F., and Uren, J., 1989, Laser surveying: London, Van
Nostrand Reinhold (International), 256 p.
Contains a good description of the basics of lasers, particularly
GaAs diodes, and a clear description of the basics of EDMs. Covers other
types of laser equipment as well (e.g., timed pulse distance measurement,
alignment lasers, and laser Theodolites and levels), and laser safety
(TA579.P94 1989, Engineering Library).
Basic Surveying
Moffitt, F. H., and Bouchard, H.,
1987, Surveying: New York, Harper and Row, 876 p.
Good reference on the subject. This one has it all (8th edition,
TA545.B7 1987, Engineering Library).
Advanced Surveying
Kennie, T. J. M., and Petrie, G.,
editors, 1990, Engineering surveying technology: New York, John Wiley and
Sons (Halsted Press), 485 p.
Thorough overview of latest advances. Contains nice discussions of
electronic distance and angle measurement, survey network errors,
photogrammetry, and digital terrain modeling
Mapping reference
Antonellini, M., Arrowsmith, R.,
Aydin, A., Christiansen, P., Cooke, M., Cruikshank, K., Du, Y., and Wu,
H., 1992, Complex surface rupture associated with the North Emerson Lake
fault zone, caused by the 1992 Landers, CA earthquake: results of
detailed mapping: EOS Transactions AGU, v. 73, p. 362.
Comments? e-mail Dr. Ramón Arrowsmith ramon.arrowsmith@asu.edu







 x 4
x 4 
















 or
or 







 . The EDM will measure the slope distance in about 3 seconds, and it will
display on the LCD of the EDM if you push
. The EDM will measure the slope distance in about 3 seconds, and it will
display on the LCD of the EDM if you push 






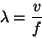 (1)
(1)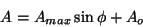 (2)
(2)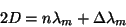 2 (3)
2 (3)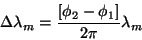 (4)
(4)
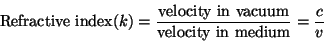 (5)
(5)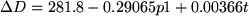 (6)
(6)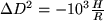 (7)
(7)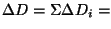 = sum of scale corrections (n is the number of scale
corrections) in ppm, and mm = prism constant in mm.
= sum of scale corrections (n is the number of scale
corrections) in ppm, and mm = prism constant in mm.





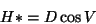
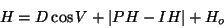 (9)
(9)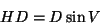 (10)
(10)
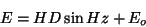 (11)
(11)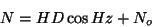 (12)
(12)


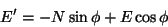 (13)
(13)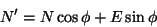 (14)
(14)

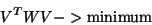 (15)
(15)
